【Cadence仿真技巧学习笔记】求解65nm库晶体管参数un, e0, Cox
- 在设计放大器的第一步就是确定好晶体管参数和直流工作点的选取。
- 通过阅读文献,我了解到L波段低噪声放大器的mos器件最优宽度计算公式为
W o p t . p = 3 2 1 ω L C o x R s Q s p W_{opt.p}=\frac{3}{2}\frac{1}{\omega LC_{ox}R_{s}Q_{sp}} Wopt.p=23ωLCoxRsQsp1 - 根据设计指标我们得知,L波段的中心频率为1.3GHz,取 ω 0 = 1.3 G H z , R s = 50 Ω , γ = 2 , δ = 4 , α = 1 , V d d = 1.2 V , L = 0.13 u m , E s a t = 4 × 1 0 6 V / m \omega_{0}=1.3\mathrm{GHz},R_{s}=50\Omega,\gamma=2,\delta=4,\quad\alpha=1,\quad V_{dd}=1.2\mathrm{V},\quad L=0.13\mathrm{um},\quad Esat=4\times10^{6}\mathrm{V/m} ω0=1.3GHz,Rs=50Ω,γ=2,δ=4,α=1,Vdd=1.2V,L=0.13um,Esat=4×106V/m
- 进而我们可以得到最优品质因子Qsp为4
- 那么我们还剩下单位面积栅氧化层电容Cox是未知量
- 下面我介绍两种求解得到Cox的方法
方法一:寻找
- 以tsmcN65工艺库为例,找到工艺库对应的参数文件,其路径为


- 打开后先搜索对应的晶体管,这里我使用到的晶体管是nmos_rf,
- 可以看到,在这个工艺库模型文件中,其定义说明了晶体管的nr,lr,wr的范围,并说明了其额定工作电压为1v。

- 然后搜索相对真空介电常数epsrox,其值为3.9,这是表示SiO₂ 的介电常数

- 然后搜索等效栅氧化层厚度toxe,其值为2E-9,

- 载流子迁移率:u0,其值为0.02232

- 然后根据单位面积栅氧化层电容公式
C o x = ϵ o x t o x C_{ox}=\frac{\epsilon_{ox}}{t_{ox}} Cox=toxϵox - 其中 ϵ o x \epsilon_{ox} ϵox是 SiO₂ 的介电常数,通常取值:
ϵ o x = 3.9 × ϵ 0 = 3.9 × 8.854 × 1 0 − 12 F / m ≈ 3.45 × 1 0 − 11 F / m \epsilon_{ox}=3.9\times\epsilon_0=3.9\times8.854\times10^{-12}\mathrm{F/m}\approx3.45\times10^{-11}\mathrm{F/m} ϵox=3.9×ϵ0=3.9×8.854×10−12F/m≈3.45×10−11F/m - tox是氧化层厚度,取决于 CMOS 工艺节点。例如:
∙ t o x ≈ 2 n m = 2 × 1 0 − 9 m ( 65 n m 工艺 ) \bullet\quad t_{ox}\approx2\mathrm{nm}=2\times10^{-9}\mathrm{m}(65\mathrm{nm}\text{工艺}) ∙tox≈2nm=2×10−9m(65nm工艺)
∙ t o x ≈ 1.5 n m = 1.5 × 1 0 − 9 m ( 45 n m 工艺 ) \bullet\quad t_{ox}\approx1.5\mathrm{nm}=1.5\times10^{-9}\mathrm{m}(45\mathrm{nm}\text{工艺}) ∙tox≈1.5nm=1.5×10−9m(45nm工艺)
∙ t o x ≈ 1.2 n m = 1.2 × 1 0 − 9 m ( 32 n m 工艺 ) \bullet\quad t_{ox}\approx1.2\mathrm{nm}=1.2\times10^{-9}\mathrm{m}(32\mathrm{nm}\text{工艺}) ∙tox≈1.2nm=1.2×10−9m(32nm工艺) - 最终可得
C o x = 3.45 × 1 0 − 11 2.5 × 1 0 − 9 = 1.38 × 1 0 − 2 F / m 2 C_{ox}=\frac{3.45\times10^{-11}}{2.5\times10^{-9}}=1.38\times10^{-2}\mathrm{F/m}^{2} Cox=2.5×10−93.45×10−11=1.38×10−2F/m2
方法二:ADE打印
- 首先搭建好晶体管的仿真电路图

- 然后进行dc直流仿真

- 运行仿真后点击Tools->Results Browser

- 在左侧栏的model文件夹下找到对应的晶体管,然后就可以找到对应的模型参数了

相关文章:

【Cadence仿真技巧学习笔记】求解65nm库晶体管参数un, e0, Cox
在设计放大器的第一步就是确定好晶体管参数和直流工作点的选取。通过阅读文献,我了解到L波段低噪声放大器的mos器件最优宽度计算公式为 W o p t . p 3 2 1 ω L C o x R s Q s p W_{opt.p}\frac{3}{2}\frac{1}{\omega LC_{ox}R_{s}Q_{sp}} Wopt.p23ωLCoxRs…...

【RocketMQ】RocketMq之IndexFile深入研究
一:RocketMq 整体文件存储介绍 存储⽂件主要分为三个部分: CommitLog:存储消息的元数据。所有消息都会顺序存⼊到CommitLog⽂件当中。CommitLog由多个⽂件组成,每个⽂件固定⼤⼩1G。以第⼀条消 息的偏移量为⽂件名。 ConsumerQue…...

小白零基础--CPP多线程
进程 进程就是运行中的程序线程进程中的进程 1、C11 Thread线程库基础 #include <iostream> #include <thread> #include<string>void printthread(std::string msg){std::cout<<msg<<std::endl;for (int i 0; i < 1000; i){std::cout<…...

利用deepseek参与软件测试 基本架构如何 又该在什么环节接入deepseek
利用DeepSeek参与软件测试,可以考虑以下基本架构和接入环节: ### 基本架构 - **数据层** - **测试数据存储**:用于存放各种测试数据,包括正常输入数据、边界值数据、异常数据等,这些数据可以作为DeepSeek的输入&…...
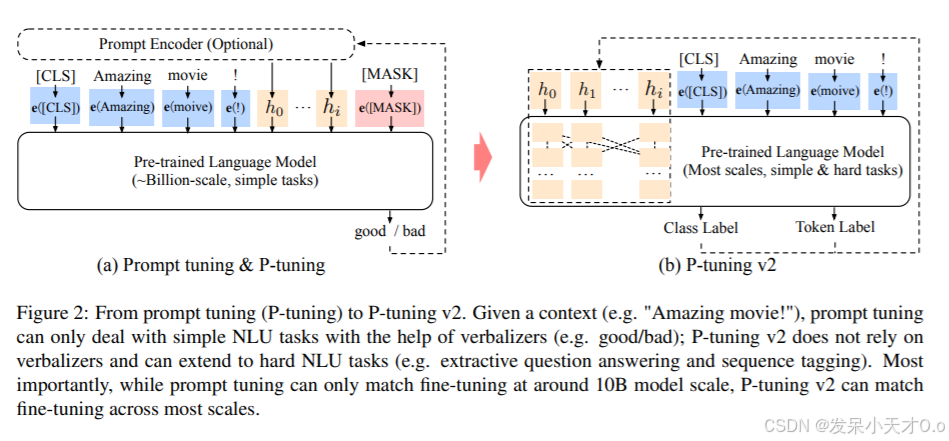
大模型微调技术总结及使用GPU对VisualGLM-6B进行高效微调
1. 概述 在深度学习中,微调(Fine-tuning)是一种重要的技术,用于改进预训练模型的性能。在预训练模型的基础上,针对特定任务(如文本分类、机器翻译、情感分析等),使用相对较小的有监…...

WPF进阶 | WPF 样式与模板:打造个性化用户界面的利器
WPF进阶 | WPF 样式与模板:打造个性化用户界面的利器 一、前言二、WPF 样式基础2.1 什么是样式2.2 样式的定义2.3 样式的应用 三、WPF 模板基础3.1 什么是模板3.2 控件模板3.3 数据模板 四、样式与模板的高级应用4.1 样式继承4.2 模板绑定4.3 资源字典 五、实际应用…...

Java 大视界 -- Java 大数据在自动驾驶中的数据处理与决策支持(68)
💖亲爱的朋友们,热烈欢迎来到 青云交的博客!能与诸位在此相逢,我倍感荣幸。在这飞速更迭的时代,我们都渴望一方心灵净土,而 我的博客 正是这样温暖的所在。这里为你呈上趣味与实用兼具的知识,也…...
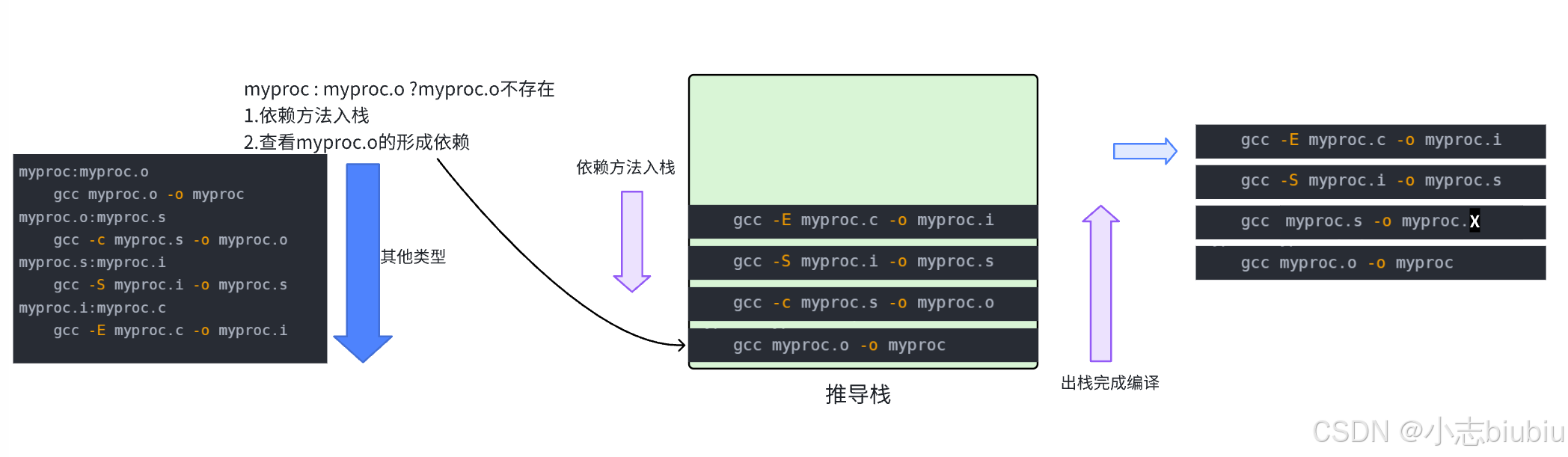
自动化构建-make/Makefile 【Linux基础开发工具】
文章目录 一、背景二、Makefile编译过程三、变量四、变量赋值1、""是最普通的等号2、“:” 表示直接赋值3、“?” 表示如果该变量没有被赋值,4、""和写代码是一样的, 五、预定义变量六、函数**通配符** 七、伪目标 .PHONY八、其他常…...

python学opencv|读取图像(五十二)使用cv.matchTemplate()函数实现最佳图像匹配
【1】引言 前序学习了图像的常规读取和基本按位操作技巧,相关文章包括且不限于: python学opencv|读取图像-CSDN博客 python学opencv|读取图像(四十九)原理探究:使用cv2.bitwise()系列函数实现图像按位运算-CSDN博客…...
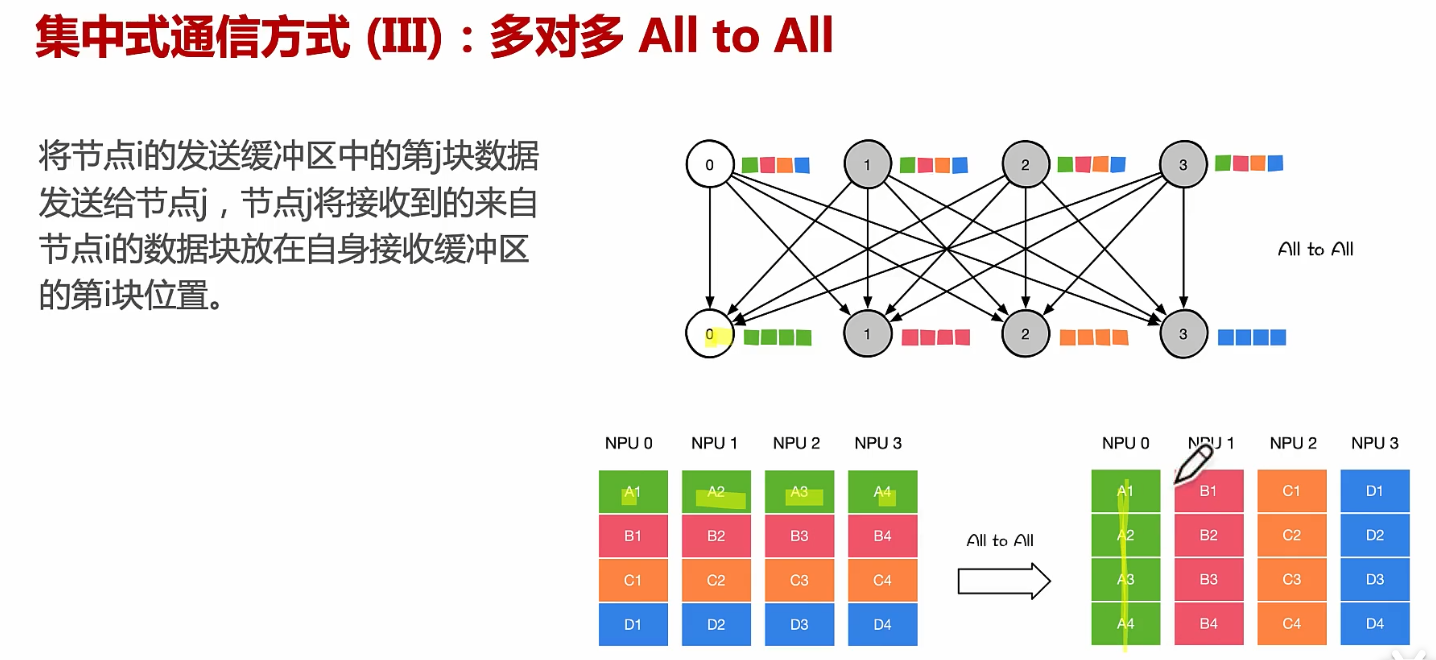
通信方式、点对点通信、集合通信
文章目录 从硬件PCIE、NVLINK、RDMA原理到通信NCCL、MPI原理!通信实现方式:机器内通信、机器间通信通信实现方式:通讯协调通信实现方式:机器内通信:PCIe通信实现方式:机器内通信:NVLink通信实现…...

TCP编程
1.socket函数 int socket(int domain, int type, int protocol); 头文件:include<sys/types.h>,include<sys/socket.h> 参数 int domain AF_INET: IPv4 Internet protocols AF_INET6: IPv6 Internet protocols AF_UNIX, AF_LOCAL : Local…...

OpenAI 实战进阶教程 - 第七节: 与数据库集成 - 生成 SQL 查询与优化
内容目标 学习如何使用 OpenAI 辅助生成和优化多表 SQL 查询了解如何获取数据库结构信息并与 OpenAI 结合使用 实操步骤 1. 创建 SQLite 数据库示例 创建数据库及表结构: import sqlite3# 连接 SQLite 数据库(如果不存在则创建) conn sq…...

Apache Iceberg数据湖技术在海量实时数据处理、实时特征工程和模型训练的应用技术方案和具体实施步骤及代码
Apache Iceberg在处理海量实时数据、支持实时特征工程和模型训练方面的强大能力。Iceberg支持实时特征工程和模型训练,特别适用于需要处理海量实时数据的机器学习工作流。 Iceberg作为数据湖,以支持其机器学习平台中的特征存储。Iceberg的分层结构、快照…...
QT交叉编译环境搭建(Cmake和qmake)
介绍一共有两种方法(基于qmake和cmake): 1.直接调用虚拟机中的交叉编译工具编译 2.在QT中新建编译套件kits camke和qmake的区别:CMake 和 qmake 都是自动化构建工具,用于简化构建过程,管理编译设置&…...
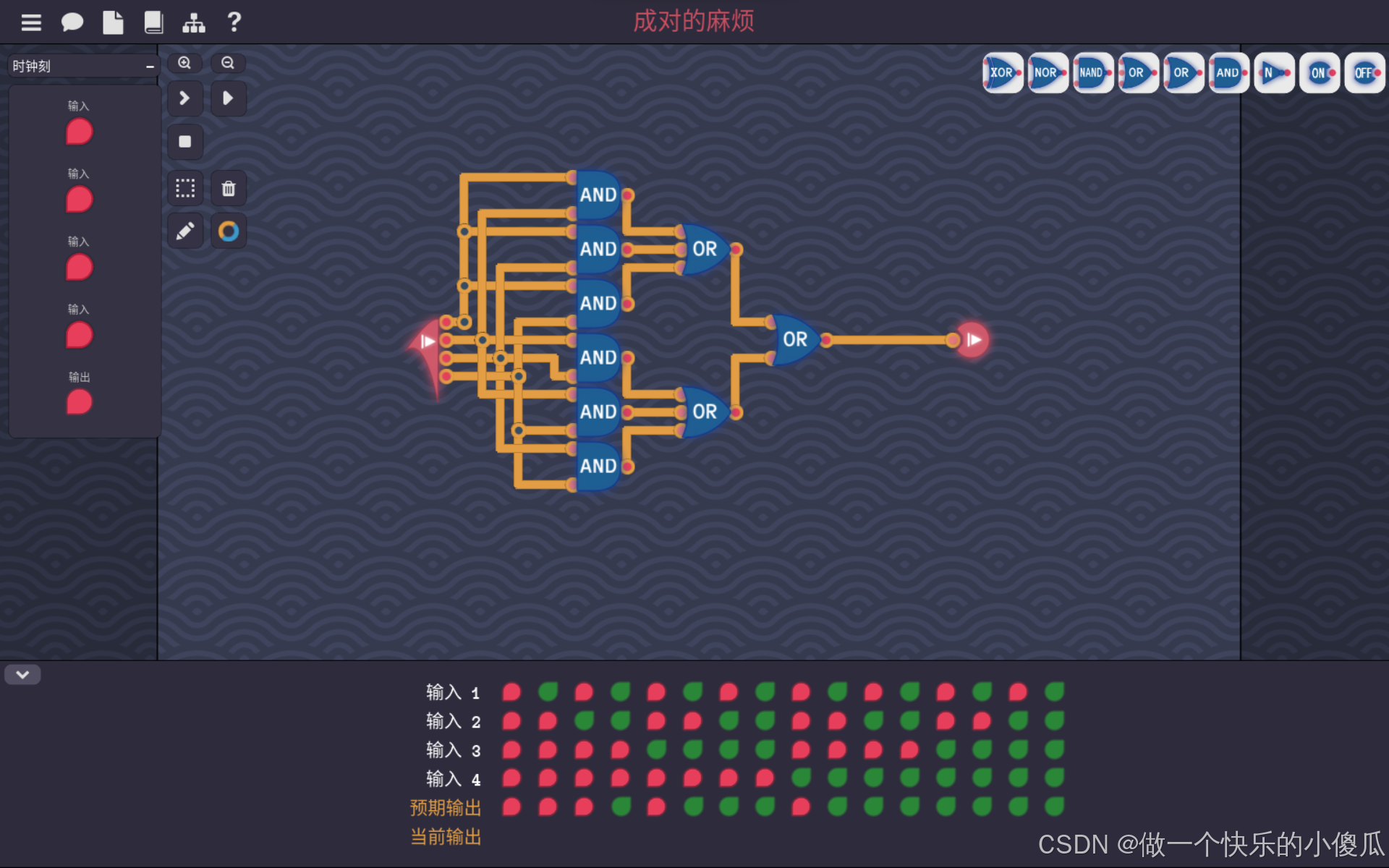
Turing Complete-成对的麻烦
这一关是4个输入,当输入中1的个数大于等于2时,输出1。 那么首先用个与门来检测4个输入中,1的个数是否大于等于2,当大于等于2时,至少会有一个与门输出1,所以再用两级或门讲6个与门的输出取或,得…...

寒假刷题Day20
一、80. 删除有序数组中的重复项 II class Solution { public:int removeDuplicates(vector<int>& nums) {int n nums.size();int stackSize 2;for(int i 2; i < n; i){if(nums[i] ! nums[stackSize - 2]){nums[stackSize] nums[i];}}return min(stackSize, …...
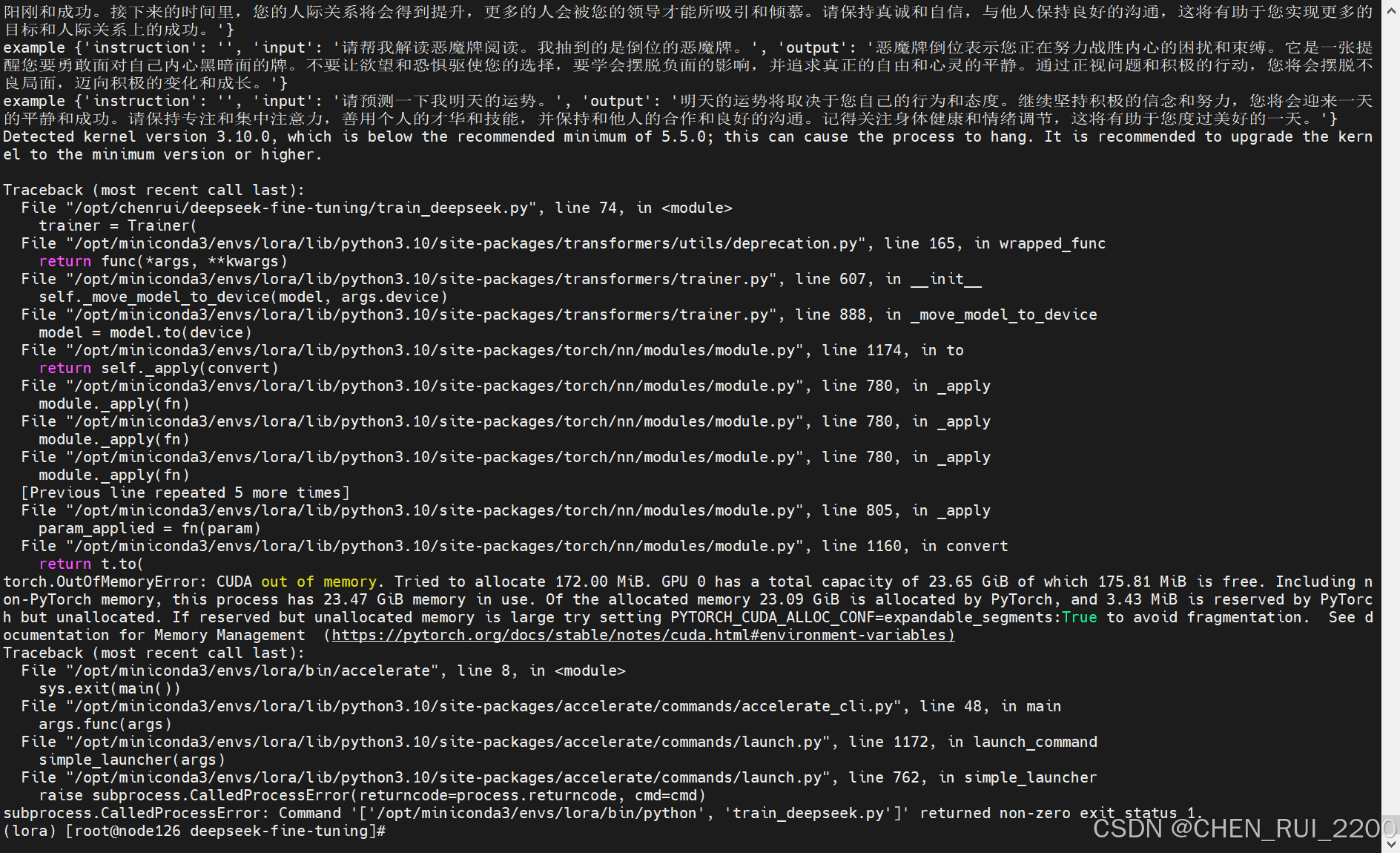
deepseek 本地化部署和小模型微调
安装ollama 因为本人gpu卡的机器系统是centos 7, 直接使用ollama会报 所以ollama使用镜像方式进行部署, 拉取镜像ollama/ollama 启动命令 docker run -d --privileged -v ollama:/root/.ollama -p 11434:11434 --name ollama ollama/ollama 查看ollama 是否启动…...

【Java异步编程】基于任务类型创建不同的线程池
文章目录 一. 按照任务类型对线程池进行分类1. IO密集型任务的线程数2. CPU密集型任务的线程数3. 混合型任务的线程数 二. 线程数越多越好吗三. Redis 单线程的高效性 使用线程池的好处主要有以下三点: 降低资源消耗:线程是稀缺资源,如果无限…...

makailio-alias_db模块详解
ALIAS_DB 模块 作者 Daniel-Constantin Mierla micondagmail.com Elena-Ramona Modroiu ramonaasipto.com 编辑 Daniel-Constantin Mierla micondagmail.com 版权 © 2005 Voice Sistem SRL © 2008 asipto.com 目录 管理员指南 概述依赖 2.1 Kamailio 模块 2.2 外…...
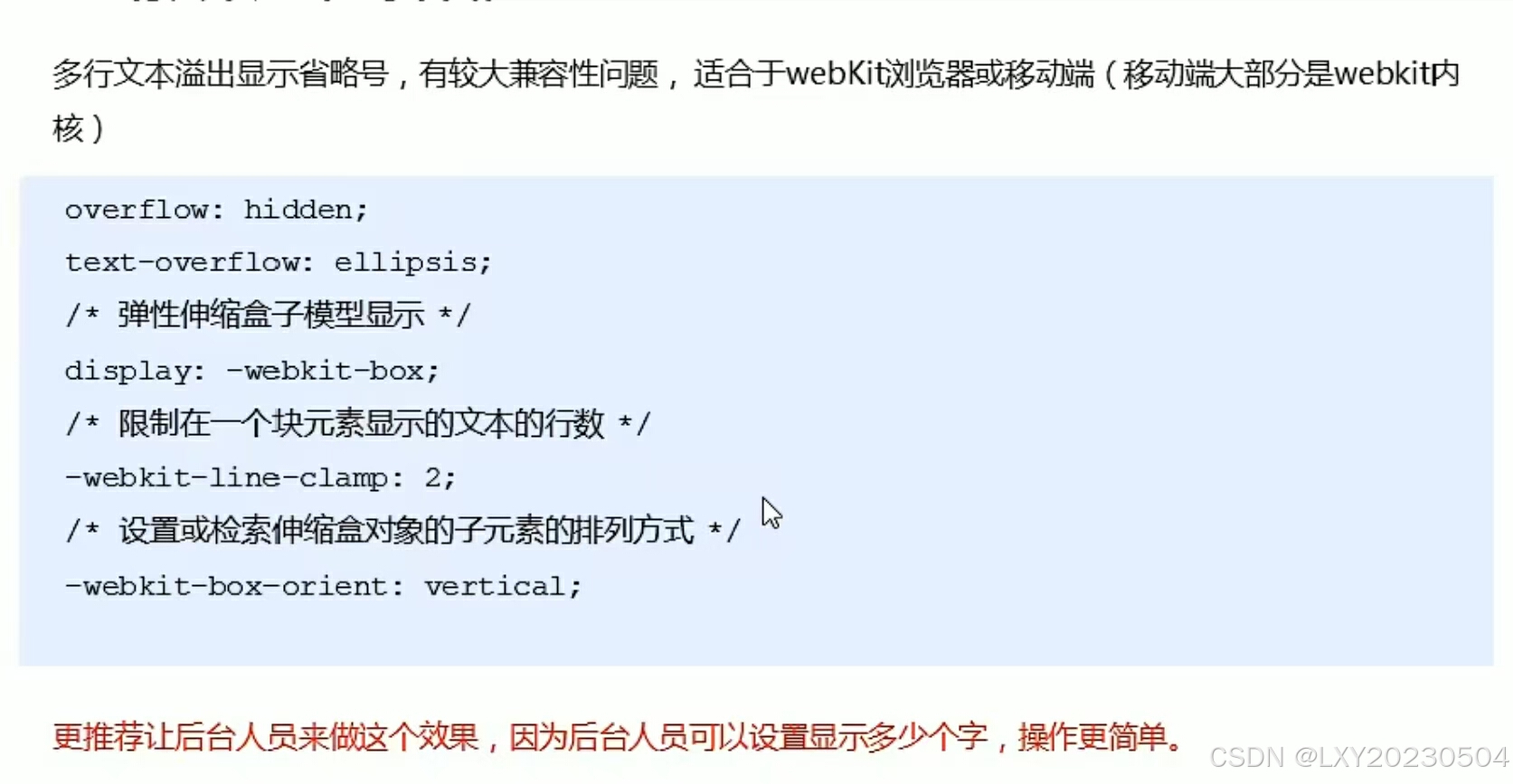
文字显示省略号
多行文本溢出显示省略号...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...
)
window 显示驱动开发-如何查询视频处理功能(三)
D3DDDICAPS_GETPROCAMPRANGE请求类型 UMD 返回指向 DXVADDI_VALUERANGE 结构的指针,该结构包含特定视频流上特定 ProcAmp 控件属性允许的值范围。 Direct3D 运行时在D3DDDIARG_GETCAPS的 pInfo 成员指向的变量中为特定视频流的 ProcAmp 控件属性指定DXVADDI_QUER…...

软件工程教学评价
王海林老师您好。 您的《软件工程》课程成功地将宏观的理论与具体的实践相结合。上半学期的理论教学中,您通过丰富的实例,将“高内聚低耦合”、SOLID原则等抽象概念解释得十分透彻,让这些理论不再是停留在纸面的名词,而是可以指导…...
