再写CentOS7升级OpenSSL-1.0.1U
本文在CentOS7.4以及TencentOS 2.4上测试通过。
原系统自带OpenSSL 1.0.2k-fips。
编译安装方法跟之前的没啥区别。
从官网下载1.0.1u版https://www.openssl.org/source/
使用tar解包
tar xfz openssl-1.0.1u.tar.gz
依次执行如下:
cd openssl-1.0.1u
./config shared zlib
make && make install
以上执行完毕,开始修改配置。
#重命名原来的openssl命令
mv /usr/bin/openssl /usr/bin/openssl.old
#重命名原来的openssl目录
mv /usr/include/openssl/ /usr/include/openssl.old
#将安装好的openssl 的openssl命令软连到/usr/bin/openssl
ln -s /usr/local/ssl/bin/openssl /usr/bin/openssl
#将安装好的openssl 的openssl目录软连到/usr/include/openssl
ln -s /usr/local/ssl/include/openssl /usr/include/openssl
#修改系统自带的openssl库文件,如/usr/local/lib64/libssl.so(根据机器环境而定) 软链到升级后的libssl.so
ln -s /usr/local/ssl/lib/libssl.so /usr/local/lib64/libssl.so
注意:这里有可能出现一个问题,就是安装完毕之后发现 /usr/local/ssl/lib/下没有so文件。我的做法是用一台纯净的CentOS虚拟机编译升级openssl,然后将so文件复制过来。
#在/etc/ld.so.conf文件中写入openssl库文件的搜索路径
echo "/usr/local/ssl/lib" >> /etc/ld.so.conf
#使修改后的/etc/ld.so.conf生效
ldconfig -v
测试
下面的特别重要,且有一定风险。
此时因为动态库没有更新,所以其他软件调用会出现调用旧版openssl的情况。
比如:

修改动态库之前现需要备份原来的动态库。
cd /usr/lib64
cp libcrypto.so.1.0.2k /root && cp libssl.so.1.0.2k /root
注:这里备份到root的根目录,其它目录也可。
cp /usr/local/ssl/lib/libssl.so ./libssl.so.1.0.2k && cp /usr/local/ssl/lib/libcrypto.so ./libcrypto.so.1.0.2k && ldconfig -v
连续执行3个命令之后,ssh链接会断开。之后重新链接即可。

还有一种方法,操作比较麻烦,但是不会ssh掉线。
同样需要先备份源文件。
ls -l libssl*.*
rm -rf libssl.so.1.0.2k && rm -rf libssl.so && rm -rf libssl.so.10 && ln -s /usr/local/ssl/bin/libssl.so libssl.so.10 && ln -s /usr/local/ssl/bin/libssl.so libssl.so
ls -l libcrypt*.so
rm -rf libcrypto.so && rm -rf libcrypto.so.1.0.2k && ln -s /usr/local/ssl/lib/libcrypto.so libcrypto.so
ln -s /usr/local/ssl/lib/libcrypto.so libcrypto.so.10
cp /root/libssl.so.1.0.2k ./libssl.so.1.0.2k.old
cp /root/libcrypto.so.1.0.2k ./libcrypto.so.1.0.2k.old
cp /usr/local/ssl/lib/libssl.so ./libssl.so.1.0.2k.old
ln -s libssl.so.1.0.2k.old ./libssl.so.10
ln -s libssl.so.10 libssl.so.1.0.0
然后用 /usr/local/ssl/bin/libssl.so覆盖libssl.so.1.0.2k.old,用 /usr/local/ssl/lib/libcrypto.so libcrypto.so覆盖libcrypto.so.1.0.2k.old
ldconfig -v
相关文章:

再写CentOS7升级OpenSSL-1.0.1U
本文在CentOS7.4以及TencentOS 2.4上测试通过。 原系统自带OpenSSL 1.0.2k-fips。 编译安装方法跟之前的没啥区别。 从官网下载1.0.1u版https://www.openssl.org/source/ 使用tar解包 tar xfz openssl-1.0.1u.tar.gz 依次执行如下: cd openssl-1.0.1u ./con…...

HBase--技术文档--基本概念--《快速扫盲》
官网 Apache HBase – Apache HBase™ Home 阿里云hbase 云数据库HBase_大数据存储_订单风控_数据库-阿里云 云数据库 HBase-阿里云帮助中心 基本概念 HBase是一种分布式、可扩展、支持海量数据存储的NoSQL数据库。它基于Hadoop,采用列式存储方式,可…...

如何利用SFTP协议远程实现更安全的文件传输 ——【内网穿透】
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《高效编程技巧》《cpolar》 ⛺️生活的理想,就是为了理想的生活! 文章目录 1. 安装openSSH1.1 安装SSH1.2 启动ssh 2. 安装cpolar2.1 配置termux服务 3. 远程SFTP连接配置3.1 查看生成的随机公…...
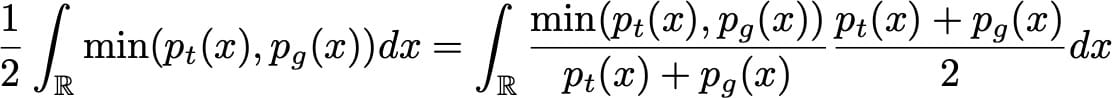
深度学习8:详解生成对抗网络原理
目录 大纲 生成随机变量 可以伪随机生成均匀随机变量 随机变量表示为操作或过程的结果 逆变换方法 生成模型 我们试图生成非常复杂的随机变量…… …所以让我们使用神经网络的变换方法作为函数! 生成匹配网络 培养生成模型 比较基于样本的两个概率分布 …...

sql入门-多表查询
案例涉及表 ----------------------------------建表语句之前翻看之前博客文章 多表查询 -- 学生表 create table studen ( id int primary key auto_increment comment id, name varchar(50) comment 姓名, no varchar(10) comment 学号 ) comment 学生表; insert…...

软考A计划-网络工程师-必考知识点-上
点击跳转专栏>Unity3D特效百例点击跳转专栏>案例项目实战源码点击跳转专栏>游戏脚本-辅助自动化点击跳转专栏>Android控件全解手册点击跳转专栏>Scratch编程案例点击跳转>软考全系列点击跳转>蓝桥系列 👉关于作者 专注于Android/Unity和各种游…...
seekToBeginning的用法)
kafka复习:(17)seekToBeginning的用法
从分区的开始进行消费,因为kafka会定期清理历史数据,所以分区开始的位移不一定为0。seekToBeginning只是从目前保留的数据中最小的offset进行消费 package com.cisdi.dsp.modules.metaAnalysis.rest.kafka2023;import org.apache.kafka.clients.consume…...
C# textBox1.Text=““与textBox1.Clear()的区别
一、区别 textbox.Text "" 和 textbox.Clear() 都可以用于清空文本框的内容,但它们之间有一些细微的区别。 textbox.Text "": 这种方式会将文本框的 Text 属性直接设置为空字符串。这样会立即清除文本框的内容,并将文本框显示为空…...

CnetSDK .NET OCR SDK Crack
CnetSDK .NET OCR SDK Crack CnetSDK.NET OCR库SDK是一款高度准确的.NET OCR扫描仪软件,用于使用手写、文本和其他符号等图像进行字符识别。它是一款.NET OCR库软件,使用Tesseract OCR引擎技术,可将字符识别准确率提高99%。通过将此.NET OCR扫…...

Python最新面试题汇总及答案
一、基础部分 1、什么是Python?为什么它会如此流行?Python是一种解释的、高级的、通用的编程语言。Python的设计理念是通过使用必要的空格与空行,增强代码的可读性。它之所以受欢迎,就是因为它具有简单易用的语法 2、为什么Pytho…...

设计模式(单例模式,工厂模式),线程池
目录 什么是设计模式? 单例模式 饿汉模式 懒汉模式 工厂模式 线程池 线程池种类 ThreadPoolExcutor的构造方法: 手动实现一个线程池 什么是设计模式? 计算机行业程序员水平层次不齐,为了让所有人都能够写出规范的代码,于是就有了设计模式,针对一些典型的场景,给出一…...

在mybatis中的mapper.xml中如何使用parameterType实现方法单个传参,对象传参,多参数传参.
在MyBatis的mapper.xml文件中,可以使用parameterType属性来指定方法的参数类型。parameterType属性用于指定传递给映射方法的参数类型,这将影响到MyBatis在映射方法执行时如何处理参数。 以下是三种不同情况下如何在mapper.xml中使用parameterType实现方…...

No120.精选前端面试题,享受每天的挑战和学习
文章目录 浏览器强制缓存和协商缓存cookie,localStorage、sessionStoragejs闭包,原型,原型链箭头函数和普通函数的区别promise的状态扭转 浏览器强制缓存和协商缓存 浏览器缓存是浏览器用于提高网页加载速度的一种机制。浏览器缓存分为强制缓…...

c# 访问sqlServer数据库时的连接字符串
//sql server 身份验证的场合, 连接字符串 private string ConnstrSqlServer "server服务器名称;uid登录名称;pwd登录密码;database数据库名称"; //windows 身份验证连接字符串 private string ConnstrWindows "server服务器名称;database数据库…...

排序算法概述
1.排序算法分类 **比较类算法排序:**通过比较来决定元素的时间复杂度的相对次序,由于其时间复杂度不能突破 O ( n l o g n ) O(nlogn) O(nlogn),因此也称为非线性时间比较类算法 **非比较类算法排序:**不通过比较来决定元素间的…...

ChatGPT在高等教育中的应用利弊探讨
人工智能在教育领域的应用日益广泛。2022年11月OpenAI开发的聊天机器人ChatGPT在全球范围内流传开来,其中用户数量最多的国家是美国(15.22%)。由于ChatGPT应用广泛,具有类似人类回答问题的能力,它正在成为许多学生和教育工作者的可信赖伙伴…...

Java之API详解之Runtime的详细解析
3.1 概述 Runtime表示Java中运行时对象,可以获取到程序运行时设计到的一些信息 3.2 常见方法 常见方法介绍 我们要学习的Object类中的常见方法如下所示: public static Runtime getRuntime() //当前系统的运行环境对象 public void exit(int statu…...

机器学习之softmax
Softmax是一个常用于多类别分类问题的激活函数和归一化方法。它将一个向量的原始分数(也称为 logits)转换为概率分布,使得每个类别的概率值在0到1之间,同时确保所有类别的概率之和等于1。Softmax函数的定义如下: 对于…...

npm script命令
1 串行/并行执行命令 //串行 npm-run-all text test npm run text && npm run test //并行改成& npm-run-all --parallel text test npm run text & npm run test2 传递参数 {"lint": "eslint js/*.js","lint:fix":…...

【力扣周赛】第360场周赛
【力扣周赛】第360场周赛 8015.距离原点最远的点题目描述解题思路 8022. 找出美丽数组的最小和题目描述解题思路 8015.距离原点最远的点 题目描述 描述:给你一个长度为 n 的字符串 moves ,该字符串仅由字符 ‘L’、‘R’ 和 ‘_’ 组成。字符串表示你在…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...

Axure Rp 11 安装、汉化、授权
Axure Rp 11 安装、汉化、授权 1、前言2、汉化2.1、汉化文件下载2.2、windows汉化流程2.3、 macOs汉化流程 3、授权 1、前言 Axure Rp 11官方下载链接:https://www.axure.com/downloadthanks 2、汉化 2.1、汉化文件下载 链接: https://pan.baidu.com/s/18Clf…...
